Bouncing ball Total time
Introduction
In this section, we will deduce the formula for the entire duration it takes for a bouncing ball to eventually stop moving. We will examine a ball with a restitution coefficient denoted as "e", initially dropped from a certain height, taking "t0" time to reach the ground. As the ball bounces, it takes different time intervals, such as t1, t2, t3, and so on, to reach successive heights after each bounce. Importantly, we assume that the time taken for ascent (going up) is the same as the time taken for descent (coming down). This results in a sequence of time intervals related to the ball's motion.
In the below figure, Seperate the Time taken when the ball is moving upward from the Time taken by the ball when moving downward by draging and droping the time arrows to thier respective positions in the Total time summation.
Restitution
Let's talk about the concept of Restitution and its coefficient, denoted as "e". The coefficient of Restitution, often referred to as "e", represents how much of the original velocity is retained after each bounce in a collision. In simpler terms, it tells us how "bouncy" or "elastic" a collision is.
Now, imagine a simulation that visually demonstrates the connection between the initial Approach velocity (how fast an object is moving towards the ground) and the resulting Separation Velocity (how fast the object is moving away from the ground) for different values of "e". This simulation helps us understand how different values of the restitution coefficient affect the behavior of objects during collisions.
As you noticed in the simulation, that the coefficient of Restitution(e) is the multiplying factor which provides the seperation velocity. And the seperation time is also obtained by multiplying the Approach time period by e(coefficient of Restitution). This relationship is shown below.

Geometric Series
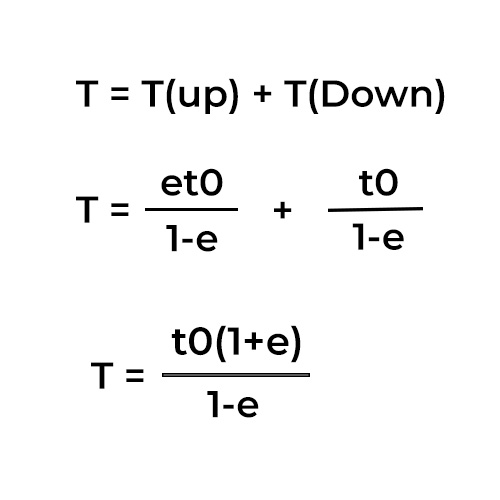
Now, with this realtionship we can express all the time intervals of all the bounces t1, t2, t3, t4..... only in terms of t0 and e, because of this we won't need to measure each and every time interval, thus helping us write a conscise equation rather than a lengthy infinite summation.
Therfore, In the below task you would need to express each of the time periods in terms of t0 with a multiplying factor.
Hint: If you want to write sqaures such as, 12 use the notation 1^2.
From the above simulation, you were able to understand how the various time intervals can be expressd in terms of "t0" and "e". Now, It is time to put it all together in the Total upward time and the Total downward time equations to see what form they will take.
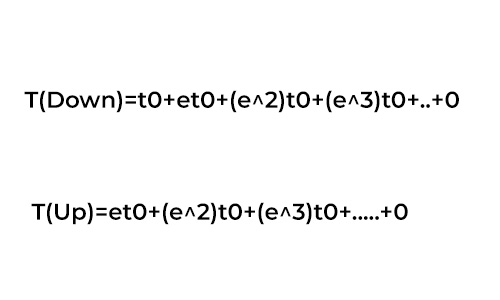
Now, the entire equation has only "t0" and "e" terms, and they are in the form of geomentric series with common ratio, e < 1. Thus, by simply applying the geomentic series equation and simplifying, We can get the desired equation for the total time taken by the bouncing ball to come to rest.